希尔伯特空间

等量变换

概率场景：

由于概率分布的积分对应面积为1，所以在微分角度上，两个分布的变化量是相等的，则有：
$$
p(x)dx=p(y)dy \
p(y)=p(x)\left|\frac{dx}{dy}\right|
$$

Hilbert Space 希尔伯特空间

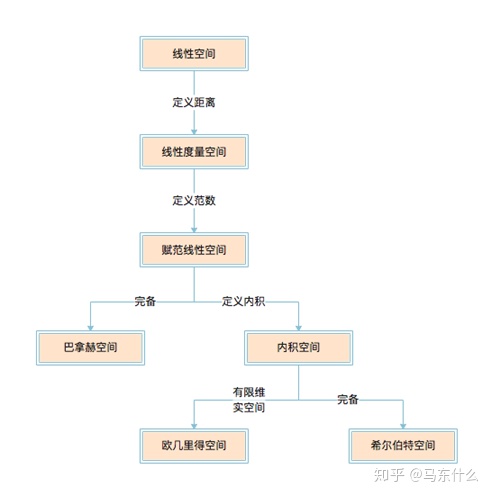
线性空间（向量空间）关注的是向量的位置，对于一个线性空间，知道基（相当于三维空间中的坐标系）便可确定空间中元素的坐标（即位置）；线性空间只定义了加法和数乘运算。

• 赋范线性空间：如果我们想知道向量的长度，定义范数

• 度量空间：如果我们想知道向量间的距离，定义距离

• 内积空间：如果我们想知道向量的夹角，定义内积

• 欧式空间：定义了内积的有限维实线性空间

  有限维：设$A$是线性空间$E$的一个线性无关子集，我们设$A$的维度为$D_E$。当$D_E< +\infty$时，称$E$为有限维的，否则称$E$为无限维的，即欧式空间中没有无限维的计算的概念

• 完备空间：如果我们想研究收敛性（极限），定义完备

  完备性：是在极限的基础上衍生的概念。例如在有理数集上的一个序列{1，1.4，1.41，1.414，1.4142…}，可知此序列极限为2根号2，而根号2为无理数，不属于有理数集，即有理数集不具备完备性，也就是有理数集不具备极限的概念，因为有理数集上的数都是确定的

• Banach空间：完备的赋范线性空间

• Hilbert空间：完备的内积空间（极限运算中不能跑出度量的范围；是欧式空间的一种推广；由于极限计算针对的一般是函数，所以Hilbert空间一般是指函数空间，可以定义函数的內积）

  函数的內积：我们有两个函数$f(x)$与$g(x)$与区间$[a,b]$，且两函数在该区间上可积且平方可积。则积分：$\int_a^b f(x)g(x)dx$，我们称之为函数的内积，函数的内积常记作$<f(x),g(x)>$，如果是离散的函数则我们可以直接：$\sum{f(x)\times g(x)}$，用矩阵表示就是$F(X)G(X)$

希尔伯特空间是一个完备的空间，其上所有的柯西列等价于收敛列，从而微积分中的大部分概念都可以无障碍地推广到希尔伯特空间中。

柯西序列
定义：在具有度量$d$的度量空间$S$中，一个序列为柯西序列，若其符合以下条件：
对于任意的实数$\epsilon > 0$，存在一正整数$N$，使得每当$m,n>N$时都有$d(a_m, a_n)<\epsilon$

在数学中，一个柯西列是指一个这样一个序列，它的元素随着序数的增加而愈发靠近。更确切地说，在去掉有限个元素后，可以使得余下的元素中任何两点间的距离的最大值不超过任意给定的正的常数。

柯西列的定义依赖于距离的定义，所以只有在度量空间(metric space)中柯西列才有意义。在更一般的一致空间(uniform space)中，可以定义更为抽象的柯西滤子(Cauchy filter)和柯西网(Cauchy net)。

柯西序列的重要作用是定义“完备空间”。完备空间是指一种度量空间，它的所有柯西序列（如果有的话），都收敛在这个空间自己里面。

在完备空间（complete space）中，所有的柯西列都有极限，这就让人们可以在不求出这个极限（如果存在）的情况下，利用柯西列的判别法则证明该极限是存在的。柯西列在构造具有完备性的代数结构的过程中也有重要价值，如构造实数。

1.对于在某度量空间内的柯西序列，它的极限不一定在相同的度量空间内。如有理柯西序列可导出无理极限。（事实上，一种实数构造就是用这种方法）

2.任何收敛列必然是柯西列，任何柯西列必然是有界序列。

希尔伯特空间为基于任意正交系上的多项式表示的傅立叶级数和傅立叶变换提供了一种有效的表述方式，而这也是泛函分析的核心概念之一。

Reproducing Kernel Hilbert Space再生核希尔伯特空间：

Kernel任何半正定的函数都可以作为核函数（Merrcer定理：充要条件）

Merrcer定理：所谓半正定函数$f(x_i, x_j)$，是指拥有训练数据集合$(x_1, x_2,\dots,x_n)$，我们定义一个矩阵的元素$a_{ij}=f(x_i, x_j)$，这个矩阵是半正定的，那么$f(x_i, x_j)$就成为半正定的函数。

再生核希尔伯特空间是支持监督学习（SVM）等监督学习模型的理论基础，实际上再生核希尔伯特空间就是是由核函数构成的希尔伯特空间，这里的再生指的是再生性，这里的核函数比如LibSVM中自带的几类：

1. 线性：$K(v_1,v_2)=<v_1,v_2>$
2. 多项式：$K(v_1,v_2)=(\gamma<v_1,v_2>+c)^n$
3. 高斯核：$K(v_1,v_2)=\exp(-\gamma|v_1-v_2|^2)$
4. Sigmoid：$K(v_1,v_2)=\tanh(\gamma<v_1,v_2>+c)$

设$\mathcal{X}$是输入空间(欧式空间$R^n$的子集或离散集合)，又设$\mathcal{H}$是特征空间(希尔伯特空间)，如果存在一个$\mathcal{X}$到$\mathcal{H}$的映射$\phi(x):\mathcal{X}\rightarrow\mathcal{H}$使得对所有$x,z\in\mathcal{X}$，函数$K(x,z)$满足条件$K(x,z)=\phi(x)\cdot\phi(z)$则称$K(x,z)$为核函数，$\phi(x)$为映射函数，式中$\phi(x)\cdot\phi(z)$为$\phi(x)$和$\phi(z)$的內积。

再生性指的就是原本函数之间计算内积需要算无穷维的积分（也就是这个映射函数可以映射到高维甚至无穷维（高斯核），而计算无穷维的积分是非常复杂的），但是现在只需要算核函数可以。